预约小初高体验课 享受1对1辅导
各位家长请注意:此表单用于预约体验课,不想预约的家长,请勿填写
小学数学数字分组知识点梳理,从n个不同元素中,任取m(m≤n)个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号p(n,m)表示.现在学而思1对1小编为大家整理好了小学数学数字分组知识点梳理. 咨询热线:4000-121-121
小学数学数字分组知识点梳理
 请加入QQ群,试题资料免费放送!
请加入QQ群,试题资料免费放送!

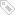 标签: 小学数学数字分组知识点梳理
标签: 小学数学数字分组知识点梳理
 保存 |
保存 |
 打印 |
打印 |
 关闭
关闭
